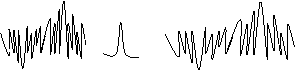Waveform Interpretation (1)
A major goal of volcano
seismology is to ascertain what physical source motions are occurring
within the volcano and/or at the surface of the volcano. In an attempt to extract
useful information from a seismogram we assume that the recorded waveform W(t)
is a linear convolution of this unknown source-time function S(t), a
propagation filter of the volcano itself (also known as a Green’s
function G(t)), and an instrument response (I(t)). The convolution is often written as W(t) =
S(t) * G(t) * I(t). Or it can be written
in the frequency domain as W(ω) = S(ω) x
G(ω) x I(ω).
The major problem is that in
seismology, and in particular in volcano seismology, is that the
Green’s function is incredibly complicated.
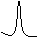
What this means is that even if we have a very simple source
function, like a delta pulse, and an instrument response that is broad-band
(a delta pulse in time series), we can still get a very complex
seismogram.
* * =
S(t) G(t) I(t)
W(t)