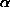 p1p2/r2
p1p2/r2Any discussion of magnetism is complicated because the physical notation for magnetic fields is not standardized.
mks-SI system regards magnetism as an effect of electric currents
- where as -
cgs system begins with forces between poles
Coulomb has shown that the forces between poles obey an inverse distance squared law, i.e.
F 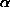 p1p2/r2
p1p2/r2
or
F =  op1p2/4
op1p2/4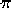
 rr2
rr2
where  o = 4
o = 4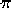 x 10-7 Webers/amp-m in the mks-SI system and 1 in the cgs
x 10-7 Webers/amp-m in the mks-SI system and 1 in the cgs
 o is the magnetic permeability of free space (i.e. vacuum)
o is the magnetic permeability of free space (i.e. vacuum) r is the relative permeability of the medium
r is the relative permeability of the mediumA unit pole strength is defined as the strength that repels an identical pole 1 cm (m) away with a force of 1 dyne (Newton) in free space (i.e. a vacuum). The force is attractive if poles are of opposite sign and repulsive if of like sign.
The magnetic field B due to a pole of strength p1 at a distance r from the pole is defined as the force per unit positive pole at that point, i.e.
B =  op1/4
op1/4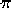
 rr2
rr2
Magnetic fields can also be defined in terms of a potential like gravity fields. Magnetic potential is defined as the work required to bring a unit pole from infinity to some point in space in the presence of a magnetic field and is given by
V =  op1/4
op1/4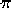
 rr
rr
The magnetic field in any direction is then given by the partial derivative of the potential in that direction.
However, it is more convenient to think of the magnetic state of a body as resulting from elementary magnets or dipoles.
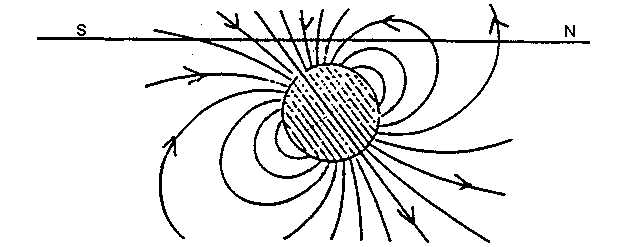
A dipole (or a bar magnet that acts as a dipole) consists of a positive (or north-seeking pole) and a negative (or a south seeking pole) pole separated by a "small" distance. A pole is where the magnetic effect is strong. A dipole generates its own magnetic field or flux and this field or flux can be mapped out from the directions assumed by a small compass needle (iron filings) suspended in the field.
Note the concentration of filings at the pole and the shape of the field lines. The North end of a compass will align itself with the field such that it points toward the South Pole of the magnet.
The strength of a dipole is termed the magnetic dipole moment, m (note this is a vector)
cgs units - gauss-cm3 (emu)
a bar magnet 1 cm long is said to have a strength of 1 gauss-cm3 if when place in a one gauss field a force of one dyne acting on each end of the dipole is required to keep the magnet perpendicular to the direction of the applied field
mks-SI units - Am2
a current loop 1 meter in cross-sectional area having a current of 1 Ampere flowing thru it has a strength of 1 Am2
1 Am2 = 103 gauss-cm3
magnetic dipole moment (m) of the Earth is 8 x 1022 Am2
The magnetic potential of a dipole is given by:
V = ( om/4
om/4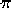 r2)cos
r2)cos
The magnetic field given by:
B = - 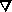 V(r)
V(r)
From the above, the radial and tangential components of the magnetic field are:
 om/4
om/4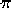 r3) sin
r3) sin 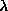 = 2(
= 2( om/4
om/4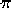 r3) cos
r3) cos 
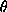 = (
= ( om/4
om/4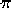 r3) cos
r3) cos 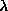 = (
= ( om/4
om/4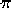 r3) sin
r3) sin 
where 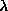 is latitude and
is latitude and  is co-latitude
is co-latitude
The total intensity of the field at a given latitude (colatitude) is given by:
B = 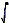 Br2 + B
Br2 + B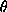 2 = (
2 = ( om/4
om/4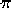 r3)(4 cos2
r3)(4 cos2 + sin2
+ sin2 )1/2
)1/2
and the inclination of the field at this location can be derived from the following:
tan I = 2 cot  = 2 tan
= 2 tan 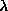
In actuality, the magnetic field can be either represented by:
- or -
1 A/m = 4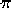 x 10-3 oersteds
x 10-3 oersteds
1 Tesla = 104 gauss
Magnetic induction (B) originates from all currents both at the microscopic (atomic) and macroscopic level and is considered the number of lines of force per cross-sectional area (i.e. flux density while magnetic field intensity (H) arises from only true currents.
B and H are useful when considering the field in the presence magnetic materials, but the magnetic field of the Earth is measured in a non-magnetic media such as air or water, therefore the equations for free space can be applied to relate B and H
mks-SI:
B =  oH where
oH where  o = 4
o = 4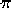 x 10-7 Webers/amp-m
x 10-7 Webers/amp-m
cgs:
B = H because  o = 1
o = 1
Intensity of magnetization, magnetic dipole moment per unit volume, or induced magnetization
when a magnetizable material is placed in a magnetic field it will become magnetized in the direction of the applied field. The intensity of this induced magnetization which we call the induced magnetization, Mi, (or magnetic dipole moment per unit volume ) is proportional to the strength of the field (and in the direction of the field) and will disappear when the field is removed.
Mi = induced magnetization, magnetic polarization, magnetic dipole moment per unit volume
(A/m - mks-SI; orested - cgs)
If Mi is constant and is in the same direction throughout the body, the body is said to be uniformly magnetized by induction.
Magnetic susceptibility
The degree to which a body becomes magnetized is determined by its magnetic susceptibility. This is the fundamental parameter in magnetic prospecting.
- or -
 o where B has units of tesla (gauss in cgs)
o where B has units of tesla (gauss in cgs)Susceptibility is both a measure of the ability of a rock to acquire a magnetization but is also a measure of the amount of magnetic material in a rock.
kSI = 4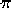 kcgs
kcgs
Magnetic fields in the presence of magnetic materials:
B =  o(H + Mi) (mks-SI) -or- B = H + 4
o(H + Mi) (mks-SI) -or- B = H + 4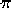 Mi (cgs)
Mi (cgs)
B =  H
H
where
 =
=  o(1 + k) =
o(1 + k) =  o
o r (mks-SI)
r (mks-SI)
where  r = 1 + k
r = 1 + k
 = 1 + 4
= 1 + 4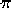 k (cgs)
k (cgs)
Diamagnetism, paramagnetism, ferromagnetism
Minerals that make up rocks are either diamagnetic, paramagnetic or ferromagnetic.
(Note: Quantum theory states that two electrons can occupy the same electron shell provided that their spins are in the opposite direction.)
diamagnetism
paramagnetism
ferromagnetism, ferrimagnetism, antiferrimagnetism
A paramagnetic material with high susceptibility is said to be a ferromagnet. In these materials the spin magnetic moments of the unpaired electrons between neighboring atoms are magnetically coupled this results in a spontaneous or permanent magnetization. Regions within a magnetic mineral or grain has the same direction of magnetization (i.e. alignment of moments occur) are called magnetic domains.
Domains are separated by domain walls therefore a single grain can be composed of a single domain (~ 1  m) to many domains
m) to many domains
in larger grains the number of domains is a function of minimizing energy and is controlled by the shape of the grain, crystalline anisotropy of the grain, and by magnetostrictive forces (strain)
Minerals loose their spontaneous magnetization as they pass through their Curie temperature at which point thermal agitation exceeds magnetic ordering.
Ferromagnetic, ferrimagnetic, and antiferrimagnetic minerals show hysteresis, i.e. irreversibility of magnetic behavior with applied field.
Magnetic Mineralogy
The minerals that are largely responsible for the magnetic properties of rocks
are within the ternary system FeO-TiO2-Fe2O3, i.e. iron-titanium oxides.
Pyrrhotite (FeS1+x, 0 < x <0.15) when present also contributes.
Remanent Magnetism
Some rocks have a permanent magnetization in addition to an induced magnetization. Remanent magnetization is a primary magnetization acquired at or shortly after the rock formed. The direction of this magnetization, Mr, may not necessary be in the direction of the induced vector.
The ratio between Mr and Mi is called the Konigsberger ratio, Q. For rocks where Q < .2 we ignore Jr.
Plutonic --> course grained metamorphic rocks: .1 < Q < 10
Volcanic --> fine grained metamorphic rocks:1 < Q < 100
Types of remanent magnetization
Elements of the Earth's magnetic field
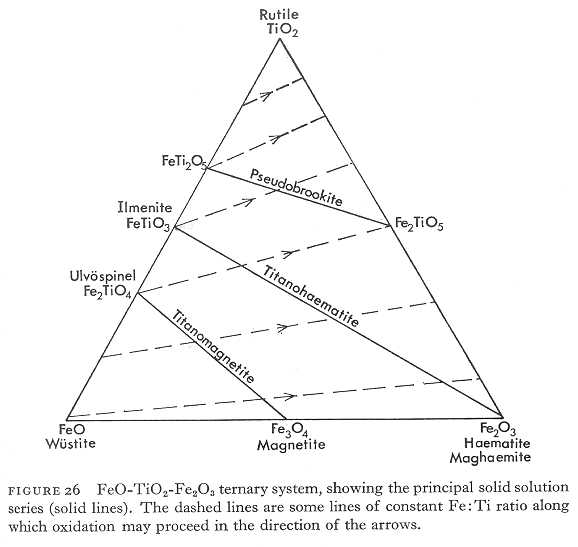
The magnetic field at any point on the Earth's surface can be described by 3 vectors and 2 angles.
The 3 vectors are:
The 2 angles are:
Equations relating these 3 vectors and 2 angles include:
H = T cosI
Z = T sinI = H tanI
X = H cosD
Y = H sinD
X2 + Y2 = H2
X2 + Y2 + Z2 = T2 = H2 + Z2
Isomagnetic maps: contour maps of equal
Magnetic dip poles -> locations on the Earth's surface where I = ±90o
The magnetic dip poles presently located at:
Geomagnetic poles -> location on the Earth's surface where the poles of a theoretical dipole (a mathematical best fit solution - IGRF) would be located
The geomagnetic poles are presently located at:
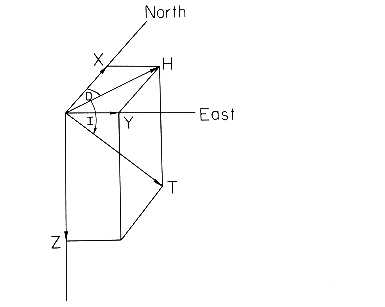
Time perturbations of Earth's magnetic field:
Corrections to Magnetometer Data
1. Diurnal variation correction
2. Temperature correction
3. Terrain correction
4. Normal correction
- or -
D
Z = Z - Zo
D
H = H - Ho
D Z anomalies
DH anomalies