
MVO/VSG - Open Scientific Meeting
27 November 1996
Elastic Models of Surface Deformation Due to Changes
in the Magma Reservoir Beneath Soufriere Hills Volcano
C.A.Williams & G. Wadge
Environmental Systems Science Centre (ESSC), University of Reading
The analytical solution to the problem of surface deformation due to a
changing pressure source buried in an elastic half space was first posed
in volcanological terms by Mogi. Such models provide a first order
picture of the deformation field due to magma withdrawal from a reservoir
supplying an eruption and supply potentially useful limits on the depth
and size of the pressurized reservoir through fitting to the observed
surface deformation. In general deformation increases in magnitude as the
reservoir gets shallower and decreases its effective area. Inversions of
observed deformation provides strong constraints on pressure/volume change
but only weak constraints on size of the reservoir.
We have taken a numerical, finite element, approach to the problem of
modelling the surface deformation at Soufriere Hills Volcano. This allows
us to take the finite size of the reservoir into account explicitly (as a
sphere). Our models are axisymmetric and elastic. They comprise 3
horizontal layers each with different material properties to mimic the
island arc crustal structure. Each finite element model has a constant
reservoir pressure change applied and the elastic response calculated to
include the effects of gravity and of topography. There are 3 main
parameter sets to be chosen for each model: the elastic parameters of the
modelling space, the pressure change based on an eruption rate from an
assumed reservoir size (e.g. 2 km radius; volume = 34 km3) and
the depth of the reservoir (chosen from a 3-21 km range at 3 km
increments). Typical choices for the pressure change would be based on an
eruption rate of about 2 x 106m3/month and the most
likely depth range is between about 6 km (minimum pressure for hornblende
stability) and about 16-17 km (depth to mid-crustal seismic velocity
discontinuity which might be a suitable location for magma ponding).
For a model with a reservoir at 16 km depth the predicted maximum surface
displacements are only of the order of a mm in magnitude for
depressurizations over a period of a month. Only if the reservoir is
shallower than the reasonable upper limit of 6 km should we expect surface
deformations at and above the level of uncertainties (about 1 cm) of the
edm and gps techniques over periods of a month or so (see first figure).
The size of the deformation network on Montserrat is of limited radial
extent (most stations are within a radius of 2-5 km of the magma
conduit). This limits the range of displacements expected for
deeper-based magma reservoirs and also any potential ability to invert the
observed shape of the deformation to a particular model. This latter
point, however, has remained academic because in 1996 at least this sort
of regional deformation field has not been observed at Soufriere Hills
Volcano. There are several possible explanations:
- the magma reservoir is deep (>>6 km),
- the chamber is not being depressurized (perhaps by magma replenishment from depth),
- the elastic model is not appropriate, and
- the deep deformation field is masked by other effects.
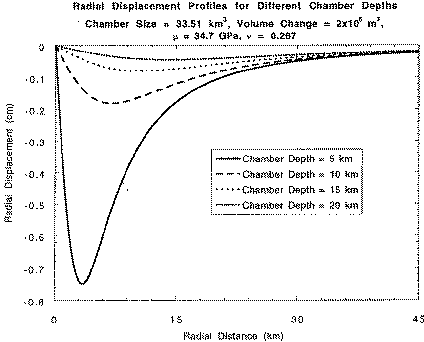
Figure 1
One possible effect that could possible account for (iv) is the surface
loading due to dome growth that must complement the evacuation at depth.
We have created some preliminary finite element models that explicitly
include this gravitational loading effect. What we find is that the
wavelength of the loading surface displacement is much shorter than the
complementary deformation effect from the reservoir such that it falls to
negligible levels at distances more than about 1 km from the dome (see
second figure). Only the Castle Peak edm reflector is within this
range. Although the shortening observed by the edm measurements from
Castle Peak to Whites and Long Ground are predicted by the model the
magnitude of the shortening is larger than that in the elastic loading
model. The software to perform this modelling has been installed at MVO
and will include the ability to calculate line length changes from any
pair of measurement stations.
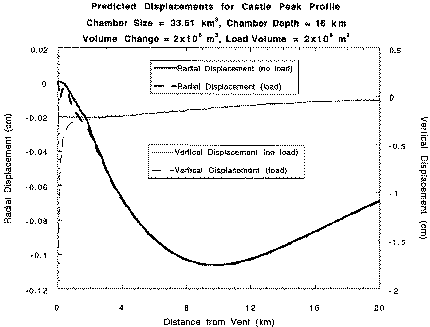
Figure 2
Montserrat Volcano Observatory


