| Michigan Tech Home | Department of Geological Engineering & Sciences | Remote Sensing Institute | MTU Volcanoes Page | Volcanic Clouds | TOMS | VAAC |

Topical Outline

Main Topics

Overview

Background

Tools

Methodology

Tutorials

Combining Data

Future

Subtopics

Background

Fluid mechanics

Simple Fluid Mechanics background
For volcanic clouds, the general "fluid" of study is the atmosphere. To determine how an ash particle falls out of the atmosphere (also called fallout), dimensionless numbers are used. These are explained below.

Reynolds Number

The atmosphere's density and viscosity decrease with altitude. Viscosity is the property of a fluid or gas which makes it resist flow. Fluids with low viscosity flow readily and vice versa. Atmospheric Density, which is defined as mass per unit volume, also affects the rate at which particles fall or settle through a fluid. These two properties are used to calculate the Reynolds number (Re) of a particle moving through the atmosphere. Reynolds number is a dimensionless number (i.e. it has no units) that is a measure of the type of flow through a fluid. In the case of falling particles, this describes the way that air flows around the particle. There are three basic types: laminar where Re < 0.4, intermediate where 0.4 < Re < 500, and turbulent where Re > 500. Note that laminar flow has streamlines that smoothly flow around the particle, while turbulent flow includes irregular eddies. See the diagrams below:

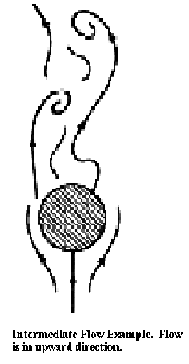
An equation for Reynolds number (Re):

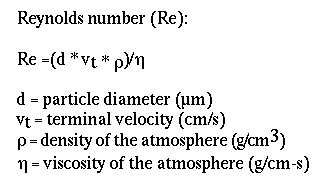
Larger pyroclasts, those >2mm in diameter, fall in a turbulent flow regime (Re> 500) through the atmosphere. Small pyroclasts, <1/16 mm, fall in laminar flow regime (Re<0.4). Intermediate size particles are transitional. These fallout relationships strongly influence atmospheric residence and fallout patterns of pyroclasts. A review of fluid principles related to particle fall is fundamental to understanding clouds, which consist of particles with low terminal velocities.

Particle Fallout

A basic equation that describes the fall of objects through the air is the gravitational settling equation. It assumes that particles falling (ash in this case) are spherical in shape. This is a broad assumption and not very accurate but is used for simplicity. This equation also assumes that these particles fall independently of each other . After a very short time, ~1-3 seconds, particles will reach a terminal velocity in earth's atmosphere, with their gravitational attraction to the earth balanced by air resistance. Small particles have dominant air resistance (fall slowly) while large particles have dominant gravity (fall rapidly). A sphere will fall through the atmosphere at a predictable terminal velocity. The equations for gravitational settling, which depend on Re are as follows:

V_t = (3.1 g r d /s)^1/2 (Re > 500) (1)

V_t = ( g r d²/ 18m) (Re< 0.4) (2)

V_t ~ d (4 r² g² / 225 ms) ^1/3 (0.4 < Re < 500) (3)

where V_t = terminal velocity of a particle, g = the gravitational acceleration, r = particle density, d = particle diameter, s = air density, and m = the dynamic viscosity.

The fall velocity of hydrometeors can be similarly predicted.

The different Reynolds Number regions correspond to the fallout deposits, according to Bonadonna et al (1998) where different slopes on a variety of plots such as ln t vs A^1/2 correspond to the various flow regimes.

Grain Size distributions

Populations of particles can be characterized by grain size distributions, which typically quantify the mass proportions of particles of different sizes. Size distributions of volcanic particles are often assumed to be log normal. Log normal distributions are known to exist for volcanic fallout.

Sources:

An interesting recent paper about the fallout of volcanic particles through earth's atmosphere is:

Bonadonna, C., Ernst G. G. J., and Sparks, R. S. J. 1998. Thickness variations and volume estimates of tephra fall deposits: the importance of particle Reynolds number: Jour Volc Geoth Res, 81: 173-184.

Diagrams were modified from this site:
Drag of Blunt Bodies and Streamlined Bodies

| Michigan Tech Home | Department of Geological Engineering & Sciences | Remote Sensing Institute | MTU Volcanoes Page | Volcanic Clouds | TOMS | VAAC|